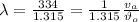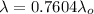Question

A sound source is moving at 80 m/s toward a stationary listener that is standing in still air (a) Find the wavelength of the sound in the region between the source and the listener (b) Find the frequency heard by the listener

Answer 1

a. wavelength of the sound,
`\vartheta = 1.315\vartheta_(o)`

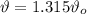
b. observed frequecy,
`\lambda = 0.7604\lambda_(o)`

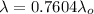
Given:

speed of sound source,
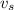`v_(s)` = 80 m/s

speed of sound in air or vacuum,
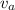`v_(a)` = 343 m/s

speed of sound observed,
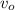`v_(o)` = 0 m/s

Solution:

From the relation:

v =
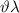`\vartheta \lambda` (1)

where

v = velocity of sound

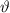`\vartheta` = observed frequency of sound

`\lambda` = wavelength

(a) The wavelength of the sound between source and the listener is given by:

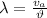`\lambda = (v_(a))/(\vartheta )` (2)

(b) The observed frequency is given by:

`\vartheta = (v_(a))/(v_(a) - v_(s))\vartheta_(o)`

`\vartheta = (334)/(334 - 80)\vartheta_(o)`

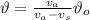
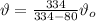
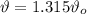`\vartheta = 1.315\vartheta_(o)` (3)

Using eqn (2) and (3):

`\lambda = (334)/(1.315) = (1)/(1.315)(v_(a))/(\vartheta_(o))`

`\lambda = 0.7604\lambda_(o)`