Question

An electron is confined in a 3.0 nm long one dimensional box. The electron in this energy state has a wavelength of 1.0 nm.

a) What is the quantum number of this electron?

b) What is the ground state energy of this electron in a box

c) What is the photon wavelength that is emitted in a transition from the energy level in part a to the first excited state?

Answer 1

Step-by-step explanation:

It is given that,

Length of one dimensional box,
`l=3\ nm=3* 10^(-9)\ m`

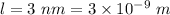
Wavelength of electron,
`\lambda=1\ nm=10^(-9)\ m`

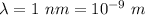
(a) We need to find the quantum number of this electron. The energy of electron in one dimensional box is given by :

`E=(n^2h^2)/(8ml^2)`

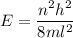
Also, energy is given by,
`E=(hc)/(\lambda)`

`(hc)/(\lambda)=(n^2h^2)/(8ml^2)`

`n^2=(8cml^2)/(h\lambda)`

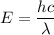
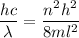
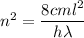
c is the speed of light

m is the mass of electron

h is the Planck's constant

`n^2=(8* 3* 10^8* 9.1* 10^(-31)* (3* 10^(-9))^2)/(6.63* 10^(-34)* 10^(-9))`

`n=√(29647.05)`

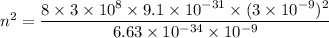
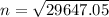
n = 172.18

or

n = 172

(b) For ground state energy, n = 1

`E=((6.64* 10^(-34))^2)/(8* 9.1* 10^(-31)* (3* 10^(-9))^2)`

`E=6.72* 10^(-21)\ J`

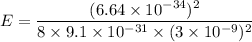
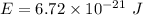
(c) We need to find the wavelength of a photon that is emitted in a transition from the energy level in part a to the first excited state (n=2). So,

`(hc)/(\lambda)=E_(172)-E_2`

`(hc)/(\lambda)=((172)^2h^2)/(8ma^2)-(4h^2)/(8ma^2)`

`(hc)/(\lambda)=(h^2)/(8ml^2)(29647.05-4)`

`(hc)/(\lambda)=(h^2)/(8ml^2)* 29643.05`

`\lambda=(8ml^2c)/(h* 29643.05)`

`\lambda=(8* 9.1* 10^(-31)* (3* 10^(-9))^2* 3* 10^8)/(6.63* 10^(-34)* 29643.05)`

`\lambda=1.0001* 10^(-9)\ m`

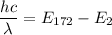
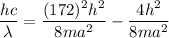
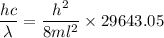
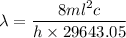
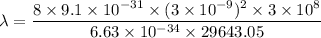
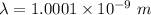
Hence, this is the required solution.