Question

Chris shoots an arrow up into the air. The height (in feet) of the arrow is given by the function h(t) = - 16t2 + 64t + 112 where t is the time in seconds. After how many seconds does the arrow reach it maximum height? Round to the nearest tenth of a second if necessary.

Answer 1

The arrow reach it maximum height after 2 seconds.

Explanation:

Chris shoots an arrow up into the air. The height (in feet) of the arrow is given by the function

`h(t)=-16t^2+64t+112`

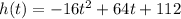
where t is the time in seconds.

In the given quadratic function, the leading coefficient is negative. It means it is a downward parabola. Vertex of a downward parabola is the point of maxima.

If a parabola is defined by
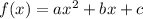`f(x)=ax^2+bx+c`, then the vertex of the parabola is

`Vertex=((-b)/(2a),f((-b)/(2a)))`

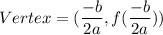
In the given function
`a=-16,b=24, c=112`.

`(-b)/(2a)=(-(64))/(2(-16))=2`

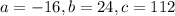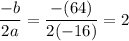
x-coordinate of vertex is 2. It means the arrow reach it maximum height after 2 seconds.

Substitute t=2 in the given function.

`h(2)=-16(2)^2+64(2)+112=176`

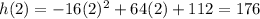
After 2 seconds the maximum height of the arrow is 176.

Answer 2

After 2 seconds

Explanation:

First step is find an equation of velocity:

h(t)=-16t2+64t+112. The velocity function is derivated from position function, so we should do that.

v(t)= h´(t)= -16*2*t+64 ⇒ v(t)= -32t+64.

Now we know the arrow reach the maximun height when this velocity is equal to zero when t>0.

0=-32t+64 ⇒ 32t=64, split each member for 32 ⇒
`(32t)/(32)`=
`(64)/(32)`

t=2. That means after 2 sec. the arrow reach the maximum height