Answer: 1.2703
Explanation:
Given : Sample size : n= 17, which is a small sample (n<30), so we use t-test.
Significance level :

Then , Critical value :

Standard deviation:
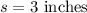
The formula to find the margin of error : -
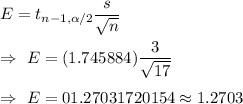
Hence, the error bound (EBM) of the confidence interval with a 90% confidence level.=1.2703