Question

The largest possible cylinder is carved out from a cube of sides 4 cm each. What is the volume of the cylinder?

Answer 1

`\text{Volume of cylinder}=16\pi\text{ cm}^3\approx 50.27\text{ cm}^3`

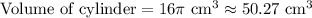
Explanation:

We have been given that the the largest possible cylinder is carved out from a cube of sides 4 cm each.

Since the cylinder is carved out from a cube of sides 4 cm each, so diameter and height of cylinder would be 4 cm each.

`\text{Volume of cylinder}=\pi r^2h`

`r=(d)/(2)=(4)/(2)=2`

`\text{Volume of cylinder}=\pi (\text{2 cm})^2* \text{4 cm}`

`\text{Volume of cylinder}=\pi*4\text{ cm}^2* \text{4 cm}`

`\text{Volume of cylinder}=\pi*16\text{ cm}^3`

`\text{Volume of cylinder}=50.265482457\text{ cm}^3`

`\text{Volume of cylinder}\approx 50.27\text{ cm}^3`

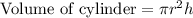
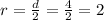
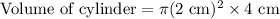
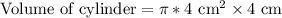
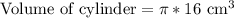
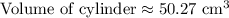
Therefore, the volume of the cylinder is approximately 50.27 cubic cm.

Answer 2

The cube has a side 4 cm long. This would mean the top of the cylinder ( circle) would have a diameter of 4 cm. and the height would also be 4 cm.

Volume of a cylinder is: Volume = πr^2h

r = radius = 4/2 = 2

h = height = 4

In terms of PI:

Volume = 2^2 x 4 x π

Volume = 16π cubic cm.

Using 3.14 for PI:

Volume = 3.14 x 2^2 x 4

Volume = 50.24 cubic cm.