Question

An air-filled solenoid has 360 turns of wire, a length of 20.0cm, and a cross- sectional area of 5.00cm^2. a) If the current is 5.00A, calculate the magnetic field in the solenoid. b) Calculate the self-inductance of the solenoid. c) If current increases at a rate of 50A per second what is the electromotive force across this solenoid?

Answer 1

(a) 0.0113 T

(b) 4.07 x 10^-4 Henry

(c) 0.02 Volt

Step-by-step explanation:

number of turns, N = 360

length, l = 20 cm = 0.2 m

Area of crossection, A = 5 cm^2 = 5 x 10^-4 m^2

i = 5 A

(a) The formula for the magnetic field of the solenoid

`B=\mu _(0)ni`

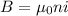
where, B be the strength of magnetic field, n be the number of turns per unit length, i be the current in the solenoid and μo is the absolute permeability of free space.

So, n = N / l = 360 / 0.2 = 1800 per metre

So, magnetic field strength

`B=4*3.14*10^(-7)*1800*5`

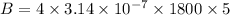
B = 0.0113 T

(b) Let L be the self inductance of the solenoid

`L =\frac {\mu _(0)N^(2)A}{l}`

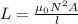
Where, N be the total number of turns, A be the area of crossection

L = 4.07 x 10^-4 Henry

(c) di / dt = 50 A/s

The relation between the electromotive force and the rate of change of current is given by

`e = - L* (di)/(dt)`

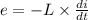
e = - 4.07 x 10^-4 x 50 = - 0.02 Volt

Negative sign shows the direction of electro motive force.