Question

A particular chemistry book costs $6 less than a particular physics book, while two such chemistry books and three such physics books cost a total of $123. Construct two simultaneous equations and solve them using substitution method.

Answer 1

Hello!

Set two variables for this situation. Let c = the cost of the chemistry book, and p = the cost of the physics book.

Create equations for the two statements seen here.

A chemistry book costs $6 less than a particular physics book: c + 6 = p

Two chemistry books and three physics book equal $123: 2c + 3p = 123

Now, set up your system of equations.

`\left \{ {{c + 6 = p} \atop {2c + 3p = 123}} \right.`

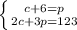
To solve, you're looking to use the substitution method. This method first takes an equation, and solves for a certain variable with it, and then substitutes in the equation for that certain variable into the other equation. That explanation was confusing, but hopefully it gets clearer here:

`\left \{ {{c + 6 = p} \atop {2c + 3p = 123}} \right.`

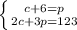
Since c + 6 = p, substitute c + 6 into the other equation for p.

2c + 3p = 123

2c + 3(c + 6) = 123

And now solve for c.

2c + 3(c + 6) = 123

2c + 3c + 18 = 123

5c = 105

c = 21

To find the other variable, just substitute c in one of the original equations.

c + 6 = p

21 + 6 = p

p = 27

Therefore, you have your solution. The chemistry book costs $21, and the physics book costs $27.

Hope this helps!