Hello!
The first thing to do is create variables. Say s = price of swiss cheese, and m = price of mozzarella.
Now, create your equations based off of the two statements given.
Six mozzarella cheeses and eight Swiss cheeses to Munga’s deli for $83.60: 6m + 8s = 83.6
Four mozzarella cheeses and four Swiss cheeses to Mina’s deli for $48: 4m + 4s = 48
Now, form your system of equations.
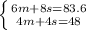
To solve this, I'm going to use elimination. This multiplies one of the equations by a certain factor, and allows the two equations to be cancelled out. That was not the best explanation, but hopefully this should help:
Multiply the bottom equation by -2 so the 2 "s's" can cancel out.
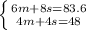

Now, add the bottom equation to the top. There is no good way to write this out in this text box, so I'll explain it - what you're doing is you're adding the individual components; add together what's on the left side of both equations, and what's on the right side of both equations.
(6m + 8s = 83.6) + (-8m - 8s = -96) -> 6m + 8s - 8m - 8s = 83.6 - 96
Now solve for m.
6m + 8s - 8m - 8s = 83.6 - 96
6m - 8m = 83.6 - 96
-2m = -12.4
m = 6.2
Now, to get s, substitute m in into one of the original equations.
4m + 4s = 48
4(6.2) + 4s = 48
24.8 + 4s = 48
4s = 23.2
s = 5.8
Therefore, swiss cheese costs $5.80 and mozzarella $6.2.
Hope this helps!