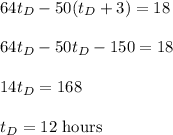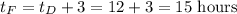Question

Fernell and Dabney shared the driving

Florida for spring break. Fernell averaged 50 mph, and
Dabney averaged 64 mph. If Fernell drove for 3 hours
longer than Dabney but covered 18 miles less than dabney, then for how many hours did Fernell drive?

Answer 1

15 hours

Explanation:

Given:

Fernell's speed
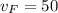`v_F= 50` mph

Dabney's speed
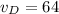`v_D= 64` mph

Denote:

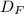`D_F` - distance covered by Fernell

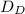`D_D` - distance covered by Dabney

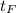`t_F` - Fernell's time

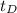`t_D` - Dabney's time

1. If Fernell drove for 3 hours longer than Dabney, then his time is 3 hours more than Dabney's time and

`t_F=t_D+3`

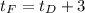
2. If Fernell covered 18 miles less than Dabney, then

`D_D-D_F=18`

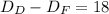
Use formula
`D=t\cdot v`

`D_D=v_D\cdot t_D\Rightarrow D_D=64\cdot t_D\\ \\D_F=v_F\cdot t_F\Rightarrow D_F=50\cdot (t_D+3)`

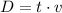
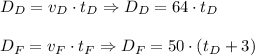
Subtract from the first equation the second equation and equate it to 18:

`64t_D-50(t_D+3)=18\\ \\64t_D-50t_D-150=18\\ \\14t_D=168\\ \\t_D=12\ \text{hours}`

`t_F=t_D+3=12+3=15\ \text{hours}`