Answer:
a. The first car wash charges more for the basic fee
b. 6 extras must be chosen for the total cost to be the same
Step-by-step explanation:
The complete question is shown in the attached diagram
The general form of the linear equation is:
y = mx + c where m is the slope and c is the y-intercept
The y-intercept represents the initial value which, in the given problem, is the basic fee
For the first car wash, we are given the equation:
y₁ = x + 9
Now, we will start by getting the equation for the second car wash:
1- getting the slope:
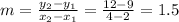
The equation now is: y = 1.5x+c
2- getting the y-intercept:
To get the y-intercept, we will simply choose a point, substitute with it in the equation from 1 and solve for c. I will use point (2,9)
y = 1.5 x + c
9 = 1.5 (2) + c ............> c = 6
The equation for the second car wash is:
y₂ = 1.5x + 6
Part 1:
As mentioned above, the y-intercept represents the basic fee
For the first car wash:
y₁ = x + 9 ................> The basic fee is $9
For the second car wash:
y₂ = 1.5x + 6 ..............> The basic fee is $6
It is clear that the basic fee for the first car wash charges more for the basic fee
Part 2:
In both equations, x represents the number of extras. We want the total cost to be the same. So, we will simply equate y₁ and y₂ and solve for x
x + 9 = 1.5x + 6
1.5x - x = 9 - 6
0.5x = 3
x = 6
Let's verify:
For x = 6:
y₁ = x + 9 = 6 + 9 = $15
y₂ = 1.5x + 6 = 1.5(6) + 6 = $15
Total cost is the same. This means that 6 extras must be chosen for the total cost to be the same
Hope this helps :)