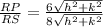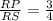Answer:
A.
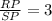
B.
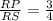
Step-by-step explanation:
The complete question is
Three collinear points on the coordinate plane are R(x, y), S(x+8h, y+8k), and P(x+6h, y+6k).
Part A: Determine the value of RP/SP
Part B: Determine the value of RP/RS
we know that
the formula to calculate the distance between two points is equal to
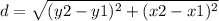
we have
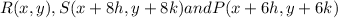
Part A.We have to find the value of
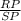
step 1
Find the distance RP
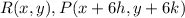
substitute the values in the formula
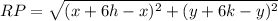
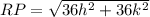
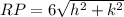
step 2
Find the distance SP
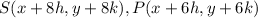
substitute the values in the formula
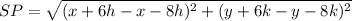
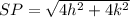
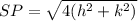
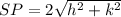
step 3
Find the ratio RP/SP
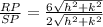
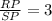
Part B. We have to determine the value of
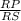
step 1
Find the distance RS
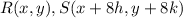
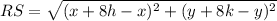
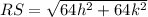
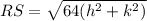
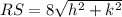
step 2
Find the ratio RP/RS