Question

A dormitory has n students, all of whom like to gossip. one of the students hears a rumor, and tells it to one of the other n − 1 students picked at random. subsequently, each student who hears the rumor tells it to a student picked at random from the dormitory (excluding, of course, himself/herself and the person from whom he/she heard the rumor). let pr be the probability that the rumor is told r times without coming back to a student who has already

Answer 1

`P(r)=((n-3)(n-4)....(n-r))/((n-2)^(r-2))`

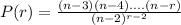
Explanation:

From the question, we have the following condition:

`p_1=p_2=1,\:and\:p_n=0`

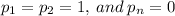
We know that each student who hears the rumor tells it to a student picked at random from the dormitory (excluding, of course, himself/herself and the person from whom he/she heard the rumor)

The 3rd student can therefore tell the rumour to n-2 students but only n-3 will accept it.

`\implies p(3)=(n-3)/(n-2)`

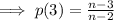
Consequently, the 4th student must not tell the 1st and second students.

`\implies p(4)=(n-3)/(n-2)* (n-4)/(n-2)`

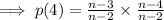
We can rewrite this to observe a pattern:

`\implies p(4)=((n-3)(n-4))/((n-2)^2)`

`\implies p(4)=((n-3)(n-4))/((n-2)^(4-2))`

`\implies p(r)=((n-3)(n-4)(n-5)...(n-r))/((n-2)^(r-2))`

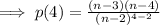
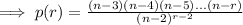
Hence, the probability that the rumor is told r times without coming back to a student who has already is:

`P(r)=((n-3)(n-4)....(n-r))/((n-2)^(r-2))`

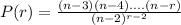
See attachment for complete question