Question

A magazine provided results from a poll of 500 adults who were asked to identify their favorite pie. Among the 500 ​respondents, 14​% chose chocolate​ pie, and the margin of error was given as plus or minus5 percentage points. Describe what is meant by the statement that​ "the margin of error was given as plus or minus5 percentage​ points." Choose the correct answer below. A. The statement indicates that the study is only 5​% confident that the true population percentage of people that prefer chocolate pie is exactly 14​%. B. The statement indicates that the study is ​100%minus5​%equals95​% confident that the true population percentage of people that prefer chocolate pie is 14​%. C. The statement indicates that the interval 14​%plus or minus5​% is likely to contain the true population percentage of people that prefer chocolate pie. D. The statement indicates that the true population percentage of people that prefer chocolate pie is in the interval 14​

Answer 1

The statement that​ "the margin of error was given as
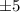`\pm5` percentage​ points" means that the population proportion is estimated to be with a certain level of confidence, within the interval
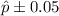`\hat{p} \pm 0.05` ; where
is likely to contain the true population percentage of people that prefer chocolate pie.

Explanation:

The margin of error for proportions is given by the following formula:

`z_(\alpha /2)*\sqrt{\frac{\hat{p}*(1-\hat{p})}{n}}`

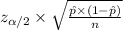
Where:

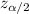`z_(\alpha /2)` is the critical value that corresponds to the confidence level; the confidence level being
`1-\alpha`,

`\hat{p}` is the sample's proportion of successes,

`n` is the size of the sample.

In this exercise we have that
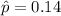`\hat{p}=0.14` and that the margin of error is 0.05.

Therefore if we replace in the formula to calculate the confidence interval we get:

`\hat{p}\pm 0.05=0.14\pm0.05=(0.09, 0.19)`

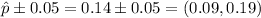
Which means that the true population proportion is estimated to be, with a certain confidence level, within the interval (0.09, 0.19).