Question

A golfball is hit from the ground with an initial velocity of 200 ft/sec. The horizontal distance that the golfball will travel, D in feet, depends on the angle in which it is hit, in radians, according to the function: Find the absolute maximum of on the applied interval [0, π/2] using the Closed Interval Method, and interpret the result in the context of the problem using a full sentence with units.

Answer 1

The golfball launched with an initial velocity of 200ft/s will travel the maximum possible distance which is 1250 ft when it is hit at an angle of
`\pi/4`.

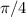Explanation:

The formula from the maximum distance of a projectile with initial height h=0, is:

`d(\theta)=(v_i^2sin(2\theta))/(g)`

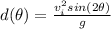
Where
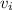`v_i` is the initial velocity.

In the closed interval method, the first step is to find the values of the function in the critical points in the interval which is
`[0, \pi/2]`. The critical points of the function are those who make
`d'(\theta)=0`:

`d(\theta)=(v_i^2\sin(2\theta))/(g)\\d'(\theta)=(v_i^2\cos(2\theta))/(g)*(2)\\d'(\theta)=(2v_i^2\cos(2\theta))/(g)`

`d'(\theta)=0\\(2v_i^2\cos(2\theta))/(g)=0\\\cos(2\theta)=0\\2\theta=\pi/2,3\pi/2,5\pi/2,...\\\theta=\pi/4,3\pi/4,5\pi/4,...`

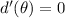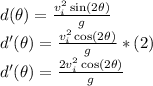
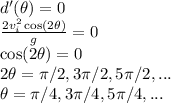
The critical value inside the interval is
`\pi/4`.

`d(\theta)=(v_i^2sin(2\theta))/(g)\\d(\pi/4)=(v_i^2sin(2(\pi/4)))/(g)\\d(\pi/4)=(v_i^2sin(\pi/2))/(g)\\d(\pi/4)=(v_i^2(1))/(g)\\d(\pi/4)=((200)^2)/(32)\\d(\pi/4)=(40000)/(32)\\d(\pi/4)=1250ft`

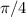The second step is to find the values of the function at the endpoints of the interval:

`d(\theta)=(v_i^2sin(2\theta))/(g)\\\theta=0\\d(0)=(v_i^2sin(2(0)))/(g)\\d(0)=(v_i^2(0))/(g)=0ft\\\theta=\pi/2\\d(\pi/2)=(v_i^2sin(2(\pi/2)))/(g)\\d(\pi/2)=(v_i^2sin(\pi))/(g)\\d(\pi/2)=(v_i^2(0))/(g)=0ft`

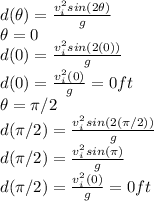
The biggest value of f is gived by
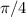`\pi/4`, therefore
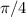`\pi/4` is the absolute maximum.

In the context of the problem, the golfball launched with an initial velocity of 200ft/s will travel the maximum possible distance which is 1250 ft when it is hit at an angle of
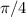`\pi/4`.