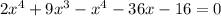Answer:
See explanation
Explanation:
Ana started the work nicely by multiplying out factors to get:\
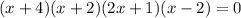
She multiplied
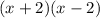 correctly using difference of two squares to get:
correctly using difference of two squares to get:
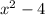
Unfortunately: She made a mistake in multiplying
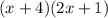 she mistakenly got
she mistakenly got
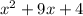 instead of
instead of
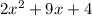 . She left out the coefficient of 2.
. She left out the coefficient of 2.
Therefore the second step should have been:
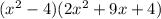
The next step will now be:
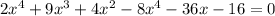
This simplifies to