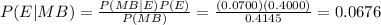Question

Customers are used to evaluate preliminary product designs. In the past, 93% of highly successful products received good reviews, 51% of moderately successful products received good reviews, and 14% of poor products received good reviews. In addition, 40% of products have been highly successful, 35% have been moderately successful and 25% have been poor products. Round your answers to four decimal places (e.g. 98.7654).(a) What is the probability that a product attains a good review?(b) If a new design attains a good review, what is the probability that it will be a highly successful product?(c) If a product does not attain a good review, what is the probability that it will be a highly successful product?

Answer 1

a. 0.5855

b. 0.6354

c. 0.0676

Explanation:

Be the events:

E: The product is highly successful

ME: The product is moderately successful

P: The product is poorly successful

B: The product received good reviews

MB: The product received bad reviews

You have then:

`P(E) = 0.4000`

`P(ME) = 0.3500`

`P(P) = 0.2500`

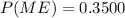
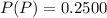
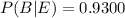`P(B|E) = 0.9300` and
`P(MB|E) = 1 - P(B|E) = 1 - 0.9300 = 0.0700`

`P(B|ME) = 0.5100`

`P(P|E) = 0.1400`

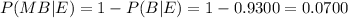
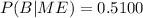
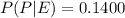
a. invoking the total probability theorem, you have:

`P(B) = P(B|E)P(E) + P(B|ME)P(ME) + P(B|P)P(P) = (0.9300)(0.4000) + (0.5100)(0.3500) + (0.1400)(0.2500) = 0.5855`

b. invoking the Baye's theorem, you have:

`P(E|B) = (P(B|E)P(E))/(P(B)) = ((0.9300)(0.4000))/(0.5855) = 0.6354`

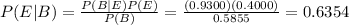
c. Using the result obtained in a.
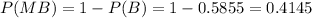`P(MB) = 1 - P(B) = 1 - 0.5855 = 0.4145`, then:

`P(E|MB) = (P(MB|E)P(E))/(P(MB)) = ((0.0700)(0.4000))/(0.4145) = 0.0676`