Answer:
B) Jane, because work does not depend on mass, only on force times distance.
Step-by-step explanation:
As we know that the force applied on two objects is of same magnitude for same interval of time
So we know that
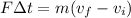
so we have
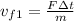
for another mass of double magnitude we have
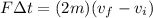
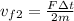
since the speed of heavy mass is half that of speed of light mass so work done must be different on two masses.
While As per Jane if two forces are same and if the cover equal distance then in that case the work done is given as
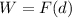
so work done would be same and it is independent of the mass of the object