Question

A bear spies some honey and takes off from rest at a rate of 2.00 m/s^2. If the honey is 9.00 m away, how fast will his snout be going at the moment of ecstasy?

Answer 1

`\rm 3√(2)\; m \cdot s^(-1)`, which is approximately 4.24 m/s.

Step-by-step explanation:

Apply the equation for constant acceleration:

`\displaystyle x = (v^(2) - u^(2))/(2a)`,

where

• 
  `x` is the displacement,
• 
  `v` is the final velocity,
• 
  `u` is the initial velocity, and
• 
  `a` is the acceleration.

For this question,

• 
  `x = \rm 9.00\; m`,
• 
  `v` the final velocity needs to be found,
• 
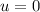  `u = 0` for the bear started from rest, and
• 
  `a = \rm 2.00\; m\cdot s^(-2)`.

Rearrange the equation:

`v^(2) = 2a\cdot x + u^(2)`,

`\begin{aligned}v &= \sqrt{2a\cdot x + u^(2)}\\ &= √(2* 2.00* 9.00)\\ &= √(18)\\&=3√(2)\\&\approx 4.24\;\rm m \cdot s^(-1) \end{aligned}\`.