Question

Please help with 8.???

Answer 1

They are inverse functions

Explanation:

A property of inverse functions is that if
`f(x) = a,  g(a) = x`

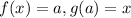
We can plug in x = 3

`f(1) = 3(3) - 2 = 7`

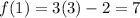
That means that, supposing they are inverse functions, g(7) should equal 3

`g(7) = (7+2)/(3) =3`

It checks out

Another way to see if two functions are inverse is to swap the x and y of one of the functions.

ex.
`y = 3x-2\\-> x = 3y - 2\\-> x+2 = 3y\\-> y = (x+2)/(3)\\ \\`

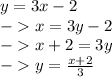
Since, after the swap, the functions are equal, we know it is an inverse function