You can solve for
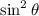 , then take square roots:
, then take square roots:
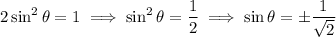
Then
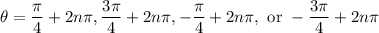
where
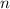 is any integer; we get the following solutions in the interval
is any integer; we get the following solutions in the interval
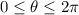 :
:
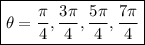
Or, you can use the double angle identity:
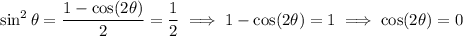
Then
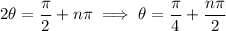
where
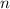 is any integer, and we get the same solutions as above within the prescribed interval.
is any integer, and we get the same solutions as above within the prescribed interval.