Question

If a quasar is moving away from us at v/c = 0.8, what is the measured redshift?

Answer 1

The measured redshift is z =2

Step-by-step explanation:

Since the object is traveling near light speed, since v/c = 0.8, then we have to use a redshift formula for relativistic speeds.

`z= \sqrt{\cfrac{c+v}{c-v}}-1`

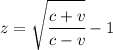
Finding the redshift.

We can prepare the formula by dividing by lightspeed inside the square root to both numerator and denominator to get

`z= \sqrt{\cfrac{1+\cfrac vc}{1-\cfrac vc}}-1`

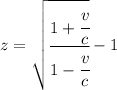
Replacing the given information

`z= \sqrt{\cfrac{1+0.8}{1-0.8}}-1`

`z= \sqrt{\cfrac{1.8}{0.2}}-1\\z= √(9)}-1\\z=3-1\\z=2`

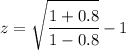
Thus the measured redshift is z = 2.