Answer:
The claim is false that the mean temperature of humans is less than 98.6°F
Explanation:
Claim :The mean temperature of humans is less than 98.6°F
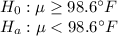
They obtained 200 measurements
Sample size n =200
x = 98.3°F
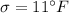
Since n > 30
So we will use z test
Formula :
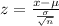
Substitute the values in the formula :
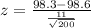
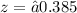
Refer the z table for p value
p value = 0.3520
α= 0.01
p value > α
So, we accept the null hypothesis.
So, the claim is false that the mean temperature of humans is less than 98.6°F .