Question

What is the upper quartile of the following set 28, 45, 12, 34, 36, 45, 19, 20

Answer 1

Q3 = 40.5

Explanation:

The first step to solve your exercise is ordering all the elements of the data set.

So the ordered data set is:

12, 19, 20, 28, 34, 36, 45, 45

The upper quartile is the median of the upper half of a data set. Mathematically, the upper quartile is the term at the position P defined by the equation below

`P = (3(n+1))/(4)`

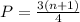
This exercise data-set has a cardinality of 8, so n = 8.

So

`P = (27)/(4)`

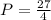
However, P = 6.75. When the decimal part is .75, we subtract .25, so P = 6.50.

So, the upper qurtily is the average between the 6th and 7th terms in the ordered set.

Uq = Q3 = (45+36)/2 = 40.5