Answer: The change in internal energy of the gas is 29.414 kJ.
Step-by-step explanation:
To calculate the temperature of the gas at different volumes, we use ideal gas equation:
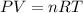
- When volume =
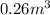
We are given:
Conversion used:
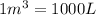
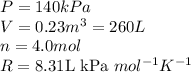
Putting values in above equation:
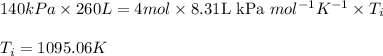
- When volume =
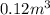
We are given:
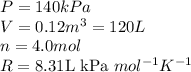
Putting values in above equation:
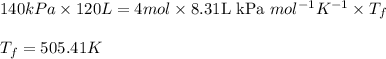
- To calculate the change in internal energy, we use the equation:
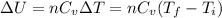
where,
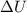 = change in internal energy = ?
= change in internal energy = ?
n = number of moles = 4.0 mol
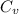 = heat capacity at constant volume =
= heat capacity at constant volume =
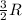
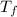 = final temperature = 1095.06 K
= final temperature = 1095.06 K
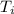 = initial temperature = 505.41 K
= initial temperature = 505.41 K
Putting values in above equation, we get:
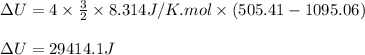
Converting this value in kilojoules, we use the conversion factor:
1 kJ = 1000 J
So,
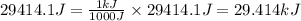
Hence, the change in internal energy of the gas is 29.414 kJ.