Question

(x^8/yz^5 )^m=1 what is the value of m

Answer 1

m = 0

Explanation:

The given expression is:

`((x^(8))/(yz^(5)))^m=1`

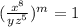
The expression on the left hand side can be equal to 1 only under two cases:

• The fractional part is equal to 1, or
• The fraction is raised to the power of 0

Case 1:

The fraction is equal to 1. Since, 1 raised to any power is equal to 1. So, in that case:
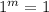`1^(m)=1`, but this would not give us the value of m. So this case is not applicable.

Case 2:

The fraction is raised to a power of 0. Any non-zero number raised to the power of 0 is always equal to 1. So, the expression would be:

`((x^(8))/(yz^(5)))^0=1`

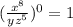
This gives us the value of m equal to 0.

From here, we can conclude that the value of m that satisfies the given equation is 0.