Question

A thin piece of wire 40 meters long is cut into two pieces. One piece is used to form a circle with radius r, and the other is used to form a square. No wire is left over. Which of the following represents the total area, in square meters, of the circular and the square regions in terms of r?

A. π∗r2π∗r2

B. π∗r2+10π∗r2+10

C. π∗r2+14∗π2∗r2π∗r2+14∗π2∗r2

D. π∗r2+(40−2π∗r)2π∗r2+(40−2π∗r)2

E. π∗r2+(10−12π∗r)2

Answer 1

Option E:
`\pi r^(2) + (10-(1)/(2) \pi r)^(2)`

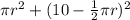
Explanation:

A 40 meters long wire is divided into two pieces. The first piece is used to form a circle of radius r and the rest of the wire is used to form a square.

First we need to find how much of the wire is used to form the circle. The total length of the wire that is used for the circle will be equal to the circumference of the circle.

Since,

Circumference = 2πr

This means 2πr meters of wire is used to form the circle and the rest is used to form the square. As the total length of the wire is 40 meters, the length of the wire that would be used to make the square will be (40 - 2πr) meters.

(40 - 2πr) meters is used to make the square, so we can say the perimeter of the square is (40 - 2πr) meters.

Since,

Perimeter of square = 4 x Length, we can write:

40 - 2πr = 4 x Length

Dividing both sides by 4, we get:

Length = 10 - 0.5πr

Now, we can find the total Area formed by circle and the square.

Area of circle = πr²

Area of Square = (Length)² = (10 - 0.5πr)²

Therefore, total area, in square meters, of the circular and the square regions in terms of r is:

`\pi r^(2) + (10-0.5\pi r)^(2)\\\\ = \pi r^(2) + (10-(1)/(2) \pi r)^(2)`

Hence, option E gives the correct answer.