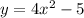2 Answers

Mjmuk · Answer 1 · 2020-07-15T22:01:38+0000

1) if you want to find the roots:

For this case we have the following quadratic equation:

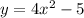
y = 4x ^ 2-5

To find the solutions we do
y = 0:

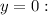
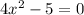
4x ^ 2-5 = 0

We add 5 to both sides of the equation:

4x ^ 2 = 5

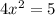
DIviding between 4 to both sides of the equation:

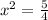
$x ^ 2 = \frac {5} {4}$

We apply square root to both sides:

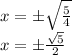
$x = \pm \sqrt {\frac {5} {4}}\\x = \pm \frac {\sqrt {5}} {2}$

Thus, the roots are:

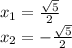
$x_ {1} = \frac {\sqrt {5}} {2}\\x_ {2} = - \frac {\sqrt {5}} {2}$

Answer:

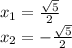
$x_ {1} = \frac {\sqrt {5}} {2}\\x_ {2} = - \frac {\sqrt {5}} {2}$

2): if you want to write the equation in vertex form:

The general quadratic equation is:

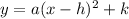
y = a(x-h)^2+k

where,

a: is the leading coefficient

(h,k): is the verex of the quadratic equation

Comparing with the original equation we have

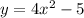
y = 4x ^ 2-5

So, the vertex is:

(h,k)=(0,-5)

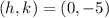
Answer

The quadratic equation in vertex form is:

Please log in or register to add a comment.