Question

Estimate the x-coordinates at which the relative maxima and relative minima occur for the function.

f(x) = 4x3 + 11x2 + 5

Question 17 options:
A. The relative maximum is at x = 1.83, and the relative minimum is at x = 0.
B. The relative maximum is at x = –1.83, and the relative minimum is at x = 1.
C. The relative maximum is at x = –1.83, and the relative minimum is at x = 0.
D. The relative maximum is at x = 1.83, and the relative minimum is at x = 1.

Answer 1

B

the answer is B

the answer is B

the answer is B

Answer 2

`\text{C. The relative maximum is at $\boxed{x = -1.83}$}\\\text{and the relative minimum is at }\boxed{x = 0}`

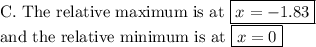
Explanation:

We could solve this problem by using calculus, but the correct answer is one of four options, so let's solve it graphically.

Create a table containing a few values of x and y.

`\begin{array}{rr}\mathbf{x} & \mathbf{y} \\-3 & -4 \\-2 & 13 \\-1 & 12 \\0 & 5 \\1&20\\\end{array}`

Plot the points and draw a smooth curve between them.

Your graph should resemble the one below.

We see that there is a local maximum between x = -1 and x = -2, probably at x ≈ -1.8.

There is a local minimum at x = 0.

`\text{The relative maximum is at $\boxed{\textbf{x = -1.83}}$}\\ \text{and the relative minimum is at }\boxed{\textbf{x = 0}}`