Question

The profit on a teddy bear can be found by using the function P(x) = - 2x2 + 35x - 99 where x is the price of the bear.Calculate the price that maximizes profit.

Answer 1

x=8.75

Explanation:

The price x that maximizes profit is the maximum value of the function, and the maximum value of the function is located at a point where the first derivative of the function is equal to zero. The first derivative is:

`P(x) = - 2x^2+35x-99\\P'(x)=-2(2)x^((2-1))+35(1)-0\\P'(x)=-4x+35`

Using P'(x)=0:

`0=-4x+35\\4x=35\\x=35/4\\x=8.75`

The minimum value of the function is also at a point where the first derivative of the function is equal to zero. To differentiate if x=8. is a minimum or a maximum obtain the second derivative and evaluate it at x=8.75 if the value P''(x)>0 x is minimum and if P''(x)<0 x is a maximum.

`P'(x)=-4x+35\\P''(x)=-4(1)\\P''(x)=-4`

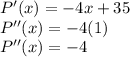
Evaluating at x=8.75:

`P''(8.75)=-4`

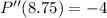
Therefore, x=8.75 is the maximum value of the function and it is the price that maximizes profit.