Question

A 6% annual coupon bond has a face value of $1,000, a market value of $1,012.73, and a yield-to-maturity of 5.87%. How many years is it until the bond matures?

Answer 1

Years until maturity date: 15

Step-by-step explanation:

We need to solve for n.

The market value of the bond is the present value of the cuopon payment and the maturity date.

PV c + PV m = $1,012.7339

The present value of the annuity:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 60

time ?

rate 0.0587

`60 * (1-(1+0.0587)^(-?) )/(0.0587) = PV\\`

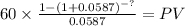
PVc

The present value of the face value at maturity date:

`(Maturity)/((1 + rate)^(time) ) = PV`

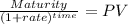
Maturity 1,000.00

time ?

rate 0.0587

`(1000)/((1 + 0.0587)^(?) ) = PV`

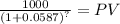
PVm

`(1000)/((1 + 0.0587)^(?) ) + 60 * (1-(1+0.0587)^(-?) )/(0.0587)= 1012.73`

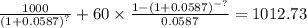
We can try to solve or do try and error

IF we use 10 as year until mature we got a market value of $1,009.6273

If we use 8 market value will be $1,008.1144

From this we got that we decrease 2 years and the market value decrease 1 dollar.

We can expect 1 dollar every 2 year.

at year 10 we have 1009 so to move to 1012 we increase 6 more years and recalculate

if N = 16 then Market value = $1,013.2558

we pass the market value, we decrease n 1 year

if n = 15 then market value = $1,012.7339

We got our given market value so 15 is the correct answer.