Question

A parallel-plate capacitor is connected to a battery. What happens to the stored energy if the plate separation is doubled while the capacitor remains connected to the battery?(a) It remains the same(b) It is doubles(c) It decreases by a factor of 2(d) It decreases by a factor of 4(e) It increases by a factor of 4

Answer 1

option (b)

Step-by-step explanation:

The capacitance of a parallel plate capacitor is given by

`C=(\varepsilon _(0)A)/(d)`

Where, A be the area of plates, d be the distance between the plates

Let the potential difference of the battery is V.

the energy stored in the capacitor is given by

`U = (1)/(2)CV^(2)`

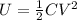
Substitute the value of C, we get

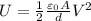`U = (1)/(2)(\varepsilon _(0)A)/(d)V^(2)` .... (1)

Now the distance between the plates is doubled, so the new capacitance

`C'=(\varepsilon _(0)A)/((d)/(2))=2C`

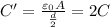
the new energy stored in the capacitor is given by

`U' = (1)/(2)C'V^(2)`

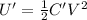
(As battery remains connected so the potential difference remains constant)

`U = (1)/(2)C'V^(2)=(1)/(2)*2CV^(2)=2U`

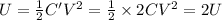
So, the energy is doubled.