Question

An object exhibits SHM with an angular frequency w = 4.0 s-1 and is released from its maximum displacement of A = 0.50 m at t = 0 s. At what time, t, does it reach its maximum speed?

Answer 1

Step-by-step explanation:

It is given that,

Angular frequency,
`\omega=4\ s^(-1)`

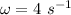
Maximum displacement, A = 0.5 m at t = 0 s

We need to find the time at which it reaches its maximum speed. Firstly, we will find the maximum velocity of the object that is exhibiting SHM.

`v_(max)=A* \omega`

`v_(max)=0.5* 4`

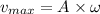
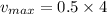
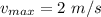`v_(max)=2\ m/s`............(1)

Acceleration of the object,
`a=\omega^2A`

`a=4^2* 0.5`

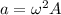
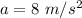`a=8\ m/s^2`...............(2)

Using first equation of motion we can calculate the time taken to reach maximum speed.

`v=u+at`

`t=(v-u)/(a)`

`t=(2-0)/(8)`

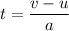
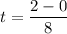
t = 0.25 s

So, the object will take 0.25 seconds to reach its maximum speed. Hence, this is the required solution.