Question

A sphere and a cube have equal volumes. The length of one edge of the cube is 1.75 meters. What is the radius of the sphere?

Answer 1

the radius is 1.08 meters

Explanation:

Hello

the volume of a cube is given by

`v_(c)=side*side*side\\\\ v=side^(3)`

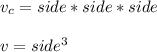
The volume of a sphere is given by:

`v_(s)=(4)/(3) \pi\ r^(3)\\`

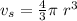
Step 1

according to the problem

`v_(c)=v_(s)\\Hence\\side^(3) =(4)/(3) \pi\ r^(3)\\`

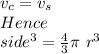
we need to know the radius, o we isolate r

`side^(3) =(4)/(3) \pi\ r^(3) \\3*side^(3) = 4 \pi \ r^(3)\\\\\ (3*side^(3))/(4 \pi ) = r^(3) \\\\r^(3) = (3*side^(3))/(4 \pi ) \\\\\ \sqrt[3]{r^(3)} =\sqrt[3]{(3*side^(3))/(4 \pi\ )} \\r=\sqrt[3]{(3*side^(3))/(4\pi)}`

Step 2

put the value of side = 1.75 into the equation

`r=\sqrt[3]{(3*side^(3))/(4\pi)}\\r=\sqrt[3]{(3*(1.75m)^(3))/(4\pi)}\\r=\sqrt[3]{(16.07)/(4\pi)}\\r=\sqrt[3]{1.27}\\ r=1.08\ m`

the radius is 1.08 meters

Have a nice day