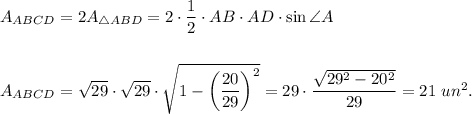Answer:
See explanation
Explanation:
Consider the parallelogram ABCD (see attached diagram). First, find the lengths of all sides:
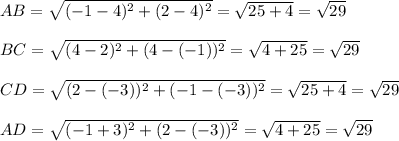
Since all sides are of equal length, this parallelogram is rhombus.
Check if it has right angles:
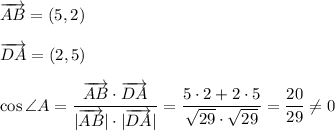
Angle A is not right angle, so this parallelogram is neither rectangle, nor square.
The perimeter is
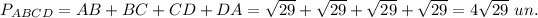
The area is