Answer:
The domain is: {x > -5 and x≠0 }
Explanation:
We are given a function f(x) and g(x) as follows:
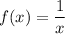
and
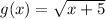
Now, the function (f/g)(x) is given by:
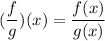
This means that:

i.e.
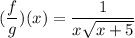
Now we know that a square root function is defined if the radicand is positive.
i.e.
Here,
x+5 ≥ 0
i.e.
x ≥ -5
Also,
x≠0 and √(x+5)≠0
( otherwise the denominator will be zero and hence the expression will be not defined)
Hence, we have:
x≠0 and x≠ -5
This means that:
x > -5 and x≠0