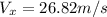Question

Car X and Y are traveling from A to B on the same route at constant speeds. Car X is initially behind Car Y, but Car X's speed is 1.25 times Car Y's speed. Car X passes Car Y at 1:30 pm. At 3:15 pm, Car X reaches B, and at that moment, Car Y is still 35 miles away from B. What is the speed of Car X?

Answer 1

26.82m/s

Step-by-step explanation:

The problem seems a little difficult, but it's not. We can start by filtering relevant information. like the relationship between their velocities, which says that Car X's speed is 1.25 times Car Y's speed. Mathematically:

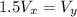`1.5V_(x) =V_(y)` or
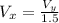`V_(x) =(V_(y))/(1.5)` (eq. 1)

We can state 1:30 pm as the initial zero time (t=0), the moment in which they're together, but car X starts to separate from Y due to its higher velocity. In parallel, we can state 3:15 pm (which corresponds to 105 minutes after 1:30 pm) as t=105 minutes, or more conveniently, t=6300s.

We have to take into account the kinematic formula:
`distance=speed*time`

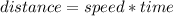
At 3600s, car X's position is B, that is:

`B=V_(x) *3600s` (eq. 2)

At that same moment, car Y's position is B minus 35 miles (56327meters)

`B-56327m=V_(y) *3600s` (eq. 3)

Replacing eq. 1 in eq. 3, and solving for B:

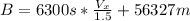`B=6300s*(V_(x))/(1.5)+56327m` (eq. 4)

Matching eq. 2 and eq. 4

`V_(x) *3600s=6300s*(V_(x))/(1.5) +56327m`

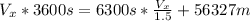
Solving for Vx:

`V_(x) =26.82m/s`

Answer 2

`v_x = 100 mph`

Step-by-step explanation:

Given

Both cars are traveling at constant speed

`v_x=1.25 * v_y`

Time when both cars are at same position
`t_o=1.30 pm`

Car X reaches B at
`t_f=3.15 pm`

Solution

Let us consider the point where both cars are at the same place as initial point. From there, time taken for car X to reach B

`\Delta t = T_f-T_o\\\\\Delta t = 3.15pm - 1.30pm\\\\\Delta t = 1 hr & 45 min\\\\\Delta t = 1.75 hour`

Distance traveled by car X in that duration

`D_x= v_x * \Delta t\\\\D_x = 1.75v_x`

Distance traveled by car Y in that duration

`D_y= v_y * \Delta t\\\\D_y = 1.75v_y`

The distance between the cars

`\Delta D = D_x-D_y\\\\35 = 1.75v_x-1.75v_y\\\\35 = 1.75(v_x-v_y)\\\\35 = 1.75 (1.25v_y - v_y)\\\\35 = 1.75(0.25v_y)\\\\v_y = 80 mph`

`v_x = 1.25 * v_y\\\\v_x = 1.25 * 80\\\\v_x = 100 mph`