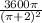Question

60 meters of fencing is used completely to form an enclosed semi-circular region. What is the area of the semi-circular region?'

Answer 1

`(3600\pi)/((\pi +2)^2)`

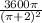
Explanation:

Given:

Perimeter of the semi-circle = 60 m

let the radius of the semi-circle to be 'r'

Also,

Perimeter of the semi-circle = πr + 2r = ( π + 2 ) × r

on equating, we get

( π + 2 ) × r = 60 m

or

r =
`(60)/((\pi +2))`

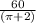
now,

the area of the semi circle = πr² / 2

on substituting the value, we get

area =
`(\pi)/(2)*((60)/((\pi +2)))^2`

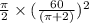
or

area =
`(3600\pi)/((\pi +2)^2)`

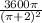
Hence,

the area of the semi-circular region =
`(3600\pi)/((\pi +2)^2)`