Answer:
Explanation:
There were 1000 trees in the first year and every year new trees are getting added.
The sequence formed for the new trees every year is
Year 1 2 3
New trees 1000 200 40
We see a geometric sequence has been formed by the new trees added
Ratio of the second year and 1st year trees added =
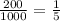
Similarly ratio of trees added in 3rd year to 2nd year =
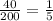
So there is a common ratio of
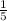
Explicit formula of a geometric sequence representing growth of the trees by
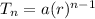
where a = number of trees grown first year
r = common ratio
n = number of years
Explicit formula showing the growth of the trees using sigma notation will be
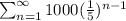
And Formula for number of trees every year will be
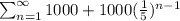
![\sum_(n=1)^(\infty)1000[1+((1)/(5))^(n-1)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/lihu8oojsdmkngbmnkhtrvlrsswlqvqgez.png)
Sum of the trees will be
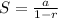
=

=
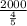
=
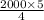
= 2500