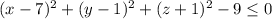Question

Write down an (in)equality which describes the solid ball of radius 3 centered at (7,1,−1). It should have a form like x2+y2+(z−2)2−4>=0, where you use one of the following symbols ≤,<,=,≥,>.

Answer 1

`(x-7)^2+(y-1)^2+(z+1)^2-9\le 0`

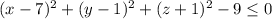
Step-by-step explanation:

A ball is the solid inside a surface which is a sphere.

The equation of a sphere has the form:

`(x-h)^2+(y-k)^2+(z-s)^2= r^2`

Where (h,k,s) is the center and r is the radius.

When we plug the given center (7,1,-1) and radius 3 we get:

`(x-7)^2+(y-1)^2+(z+1)^2= 3^2`

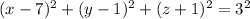
Then we turn this into an inequality: Since the ball is inside the surface we must use the
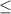`\le` symbol.

`(x-7)^2+(y-1)^2+(z+1)^2\le 9`

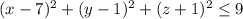
Then we just subtract 9 from both sides to get:

`(x-7)^2+(y-1)^2+(z+1)^2-9\le 0`