Question

Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its average number of unoccupied seats per flight over the past year. 225 flight records are randomly selected and the number of unoccupied seats is noted, with a sample mean of 11.6 seats and a standard deviation of 4.1 seats. How many flights should we select if we wish to estimate μ to within 5 seats and be 95 percent confident?

Answer 1

Answer: 3

Explanation:

Given : Standard deviation :
`\sigma=4.1\text{ seats}`

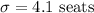
Margin of error :
`E=\pm5\text{ seats}`

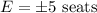
Significance level :
`\alpha: 1-0.95=0.05`

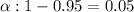
By using the standard normal table of z ,

Critical value :
`z_(\alpha/2)=1.96`

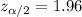
The formula we use to find the minimum sample size required :-

`n=((z_(\alpha/2)\ \sigma)/(E))^2`

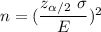
i.e.
`n=(((1.96)(4.1))/(5))^2=2.58309184\approx3`

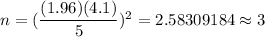
Hence, the number of lights should we select if we wish to estimate μ to within 5 seats and be 95 percent confident =3