Question

A sinusoidal wave has the following wave function: y(x,t) = (2.5 m) sin[(3.0 m-1) x – (24 s-1) t + π/2] What is the frequency of this wave?

Answer 1

3.82 Hertz

Step-by-step explanation:

`y = 2.5 Sin\left (3x-24t+(\pi )/(2)  \right )`

This is the equation of a wave which varies sinusoidally.

The standard equation of a wave is given by

`y = A Sin\left ( kx-\omega t+\phi  \right )`

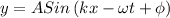
where, A be the amplitude of the wave, k be the wave number, x be the displacement of wave, ω be the angular frequency and t be the time taken, and Ф be the phase angle.

now compare the given equation by the standard equation, we get

k = 3

ω = 24

Ф = π / 2

So, the angular frequency = 24

The relation between the angular frequency and the frequency is given by

ω = 2 x π x f

24 = 2 x 3.14 x f

f = 3.82 Hertz