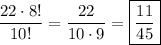Question

What is the probability of randomly choosing a permutation of the 10 digits 0, 1, 2, . . . , 9 in which (a) an odd digit is in the first position and 1, 2, 3, 4, or 5 is in the last position?

Answer 1

The first digit is one of {1, 3, 5, 7, 9}, and the last digit is one of {1, 2, 3, 4, 5}.

If the first digit is one of {1, 3, 5} (3 choices), then the last digit is one of {1, 2, 3, 4, 5} minus whatever is picked for the first digit (4 choices, and the remaining eight digits can be arranged in 8! ways, so there are 12*8! possible permutations.

If the first digit is one of {7, 9} (2 choices, then the last digit is one of {1, 2, 3, 4, 5} (5 choices), and again there are 8! ways of arranging the remaining digits, so there are 10*8! possible permutations.

Then the total number of permutations that fit the criteria is 12*8! + 10*8! = 22*8!. There are 10! total permutations that can be made overall, so the probability of randomly picking one we want is

`(22\cdot8!)/(10!)=(22)/(10\cdot9)=\boxed{(11)/(45)}`