Question

Consider a model of a hydrogen atom in which an electron is in a circular orbit of radius r = 5.92×10−11 m around a stationary proton.What is the speed of the electron in its orbit?

Answer 1

2.068 x 10^6 m / s

Step-by-step explanation:

radius, r = 5.92 x 10^-11 m

mass of electron, m = 9.1 x 10^-31 kg

charge of electron, q = 1.6 x 10^-19 C

As the electron is revolving in a circular path, it experiences a centripetal force which is balanced by the electrostatic force between the electron and the nucleus.

centripetal force =
`(mv^(2))/(r)`

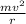
Electrostatic force =
`(kq^(2))/(r^(2))`

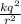
where, k be the Coulombic constant, k = 9 x 10^9 Nm^2 / C^2

So, balancing both the forces we get

`(kq^(2))/(r^(2))=(mv^(2))/(r)`

`v=\sqrt{(kq^(2))/(mr)}`

`v=\sqrt{(9* 10^(9)*1.6* 10^(-19)* 1.6* 10^(-19))/(9.1* 10^(-31)* 5.92*10^(-11))}`

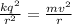
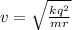
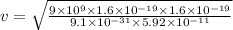
v = 2.068 x 10^6 m / s

Thus, the speed of the electron is give by 2.068 x 10^6 m / s.