Answers:
1) Sometime in 2014
As we can see in the graph in 2014 there is an intersection between the lines that represent the wind energy production of Spain and India, then the production of India is increased, while that of Spain remains constant.
2) Germany
As we can see in the graph in 2000 Germany was the number 1 producer of gigawatts of wind energy. In addition it is observed a rapid growth and increase in production compared to the other countries.
3) In 2006, America was producing over 10 GW and began a steep climb in wind energy production.
In 1997, America began with a constant and very small energy production, which was growing gradually until 2006, when its rapid growth in production began to exceed the other countries shown in the graph.
4) Years
When a function is plotted, generally the independent variable, whose value is previously set, is represented on the X axis.
In this sense, the variable found on the X axis of this graph is Years.
5) Wind Energy Capacity
When a function is plotted, generally the dependent variable (which is generated from the independent variable) is represented on the Y axis.
In this sense, the variable found on the Y axis of this graph is Wind Energy Capacity.
6) Gigawatts (GW)
We already know the dependent variable in this Wind Energy Capacity vs Years graph is Wind Energy Capacity, and its Unit is Gigawatts (GW).
Where
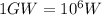
7) Both onshore and offshore wind sources
When we talk about scientific experimentation and representing data, the Control Variable is the one that remains constant (it does not change during the investigation).
According to the explanation above, the option that fits with this characteristic is: Both onshore and offshore wind sources
8) 55 GW
If we want to make a linear interpolation to estimate how much wind energy capacity was there in the United States in the middle of 2011, firstly we need to find two points where the value we want to find is in the middle.
These points (X,Y) are:
P1: (2011,48) and P2: (2012,60)
Where X1:2011, Y1:48, X2:2012, Y2:60
Now we find the slope
of the line with the following equation:
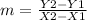
Then, with this value of the slope we can write the equation of the line and find the intersection point
with one of the given points (we will use P1):
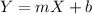
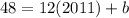
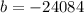
With this value and the slope, we can find Y for X=2011.5 (we need to know the wind capacity in the middle of 2011):
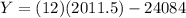
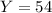This is the estimated result 54 GW, and the option that is near this value is 55 GW
9) 36 GW
In this case we will apply a similar method as the previous answer, but estimating a prediction:
Let's find two points near the value we want to find. These points (X,Y) are:
P1: (2014,22) and P2: (2016,29)
Where X1:2014, Y1:22, X2:2016, Y2:29
Now we find the slope
of the line with the following equation:
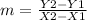
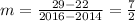
Then, with this value of the slope we can write the equation of the line and find the intersection point
with one of the given points (we will use P2):
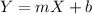
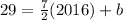
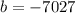
With this value and the slope, we can find Y for X=2020 (we need to estimate the expected wind capacity in 2020):
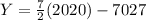
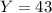This is the estimated result 43 GW (note linear extrapolation is not as accurate as other methods), and the option that is near this value is 36 GW
10) Additional 7 GW/Year
In this case we will use the equation of the slope:
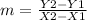
With the following points:
P1: (2009,35) and P2: (2016,82)
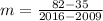
Therefore, the correct option is Additional 35 GW/Year