Answer : The cell emf for this cell is 0.118 V
Solution :
The balanced cell reaction will be,
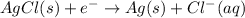
Oxidation half reaction (anode):

Reduction half reaction (cathode):

In this case, the cathode and anode both are same. So,
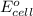 is equal to zero.
is equal to zero.
Now we have to calculate the cell emf.
Using Nernest equation :
![E_(cell)=E^o_(cell)-(0.0592)/(n)\log \frac{[Cl^-{cathode}}{[Cl^-{anode}]}](https://img.qammunity.org/2020/formulas/chemistry/college/in948yo5odepvjbnl0zl0izfv95cgll7mj.png)
![E_(cell)=E^o_(cell)-(0.0592)/(n)\log \frac{[Cl^-{diluted}}{[Cl^-{concentrated}]}](https://img.qammunity.org/2020/formulas/chemistry/college/wncdxejtma8e98l02aas1ispfr3gb2gvee.png)
where,
n = number of electrons in oxidation-reduction reaction = 1
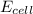 = ?
= ?
![[Cl^-{diluted}]](https://img.qammunity.org/2020/formulas/chemistry/college/bgu289gk6e7ko2ie3y3ogp8vxjnecxwsrk.png) = 0.0156 M
= 0.0156 M
![[Cl^-{concentrated}]](https://img.qammunity.org/2020/formulas/chemistry/college/3eb4ro15zuv9xt0wv0ioli2yhkk9rb6sj1.png) = 1.55 M
= 1.55 M
Now put all the given values in the above equation, we get:
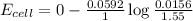
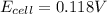
Therefore, the cell emf for this cell is 0.118 V