Question

Assume that the random variable X is normally​ distributed, with mean mu equals 100 and standard deviation sigma equals 20. Compute the probability ​P(Xgreater than116​). 0.2119 0.7881 0.2420 0.1977

Answer 1

Answer: 0.2119

Explanation:

We assume that the random variable X is normally​ distributed.

Given : Population mean :
`\mu=100`

Standard deviation :
`\sigma=20`

Z-score :
`z=(x-\mu)/(\sigma)`

Then, z-score corresponds to 116

`z=(116-100)/(20)=0.8`

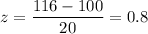
By using the standard normal distribution table for z , we have

`P(x>116)=P(z>0.8)=1-P(z\leq0.8)`

`=1-0.7881446\approx0.2119`

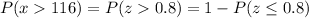
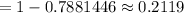
Hence, the required probability = 0.2119