Question

Let V be the volume of the solid obtained by rotating about the y-axis the region bounded y = 4x and y = x2/4 . Find V by slicing.

Answer 1

Explanation:

Consider the graphs of the
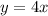`y = 4x` and
`y = (x^(2) )/(4)`.

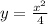By equating the expressions, the intersection points of the graphs can be found and in this way delimit the area that will rotate around the Y axis.

`4x = (x^(2) )/(4) \\   x^(2)  = 16x \\ x^(2)  - 16x = 0 \\   x(x-16) = 0` then
`x=0` o
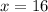`x=16`. Therefore the integration limits are:

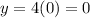`y = 4(0) = 0` and
`y = 4(16) = 64`

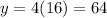
The inverse functions are given by:

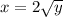`x = 2 √(y)` and
`x = (y)/(4)`. Then

The volume of the solid of revolution is given by:

`\int\limits^(64)_ {0} \, [2√(y) - (y)/(4)]^(2)  dy = \int\limits^(64)_ {0} \, [4y - y^(3/2) + (y^(2))/(16) ]\  dy = [2y^(2) - (2)/(5)y^(5/2) + (y^(3))/(48) ]\limits^(64)_ {0} = 546.133 u^(2)`