Rewrite the radical expression as an expression with rational exponents. fourth root of x to the power of 5 A.4X^5 B.5X^4 C.X^5/4 D.X^4/5

Question

asked Nov 2, 2020 200k views

2 Answers

Zord · Answer 1 · 2020-11-03T07:33:19+0000

Answer:

The correct option is C) X^(5/4).

Explanation:

Consider the provided radical expression.

$\sqrt[4]{x^5}$

Now we need to convert the radical expression into rational expression.

$a^{(m)/(n)}=(\sqrt[n]{a})^m=\sqrt[n]{x^m}$

By using the above formula we can rewrite the expression as shown:

$\sqrt[4]{x^5}$

$(\sqrt[4]{x})^5$

$(x)^{(5)/(4)}$

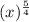
Hence, the required rational exponent is
$(x)^{(5)/(4)}$

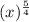
Thus, the correct option is C) X^(5/4).

Iamsamstimpson · Answer 2 · 2020-11-06T11:53:12+0000

Answer:

C

Explanation:

We simply need to remember this rule shown below:

$\sqrt[n]{x^b} =x^{(b)/(n)}$

So expression to change is
$\sqrt[4]{x^5}$

By using the law, we can rewrite this as:

$\sqrt[4]{x^5} =x^{(5)/(4)}$

Correct choice is C