Question

Rewrite the expression with rational exponents as a radical expression. 5 times x to the one fourth power

A. square root of the quantity 5 times x to the power of 4
B.fourth root of the quantity 5 times x
C. 5 times the square root of x to the power of 4
D.5 times the fourth root of x

Answer 1

D.5 times the fourth root of x

Explanation:

Given phrase,

5 times x to the one fourth power

`\implies 5* (x)^(1)/(4)`

Since, a radical expression is defined as any expression containing a radical symbol i.e. '√'

Also,

`(x)^(1)/(n)=\sqrt[n]{x}`

Hence,

`(x)^(1)/(4)=\sqrt[4]{x}`

`\implies 5* (x)^(1)/(4)=\sqrt[4]{x}`

= 5 times the fourth root of x

OPTION D is correct.

Answer 2

D

Explanation:

We need to understand the rule shown below to solve this:

`\sqrt[n]{x^b} =x^{(b)/(n)}`

The expression to change is
`5*x^{(1)/(4)}`

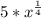
The second part can be written as (using the rule):
`x^{(1)/(4)}=\sqrt[4]{x^1}=\sqrt[4]{x}`

And since 5 is a coefficient multiplied, we simply have :
`5*\sqrt[4]{x}`

Which is "5 times the fourth root of x", D is the correct answer.