Question

he number of square feet per house are normally distributed with an unknown population mean and standard deviation. If a random sample of 47 houses is taken to estimate the mean house size, what t-score should be used to find a 80% confidence interval estimate for the population mean?

Answer 1

Answer: 1.300228

Explanation:

The t-score we use for the confidence interval is two-tailed , i.e. the t-score should be used to find a (
`1-\alpha`) is given by :-

`t_(n-1, \alpha/2)`, where n is the sample size.

Given : Level of confidence:
`1-\alpha: 0.80`

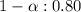
Significance level :
`\alpha: 1-0.80=0.20`

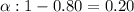
Sample size : n= 47

Then, degree of freedom :
`n-1=46`

Now by using standard normal t-distribution table,

`t_(n-1, \alpha/2)=t_(46, 0.10)=1.300228`

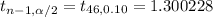
Hence, the t-score should be used to find a 80% confidence interval estimate for the population mean = 1.300228